#利用测井方法获得大地热流值
前言
大地热流的概念
大地热流简称热流,是地球内部热能传输至地表的一种现象。它是指从地球内部向地表传播的热量,传播量可以用大地热流表示,常用单位是毫瓦每平方米($mW/m^2$)。热流是描述岩石圈热结构、地球动力学过程以及评估地热资源潜力和油气成熟度的关键参数[1–3],在地质、地热资源勘查和油气开发领域都有显著意义,因而大地热流数据的测量和汇编一直是一项重要的基础工作。
自1963年国际热流委员会(IHFC)成立以来,其主要工作和业绩就是进行全球热流数据的汇编,根据其2011年发布的数据,全球热流数据共有38374个[4,5]。中国自1979年起,由中国科学院地质研究所地热组正式组织发布中国大陆地区热流数据,迄今已经完成4个版本的数据汇编发布,目前收集发布的数据有1230个(见图 1),中国科学院地质与地球物理研究所也以此为基础建立了中国大地热流数据库,并在网上发布[6–10]。
热流可以定义为:单位时间内流经单位面积的热量成为热流密度,一般可以通过地温测量和岩石热导率测试间接获得,其计算关系式为:
\[\begin{matrix} q = \lambda \cdot \frac{\text{dT}}{\text{dz}} = AD + q_{m}\ \left( \text{\ 1\ } \right) \\ \end{matrix}\]式中:$q$为热流,
$\lambda$为地层的热导率,
$\frac{\text{dT}}{\text{dz}}$为地温梯度,
$A$为岩石生热率,
$D$为地层厚度,
$q_{m}$为地幔热流。
由式1可知,在计算大地热流的过程中主要涉及两个方面的工作:一为岩石热导率测试,需要通过岩芯的测试分析获得。岩芯通常是经由取芯钻井获得,另外在测试过程中也不能忽视温度和压力改变带来的影响[11];二为地温梯度的获得,即通过温度测井从地层中获取温度,再进一步计算求得地温梯度。这个过程就要求实现精确的温度测量,需摆脱测井曲线非稳态的影响,获得更接近地层温度的数据。
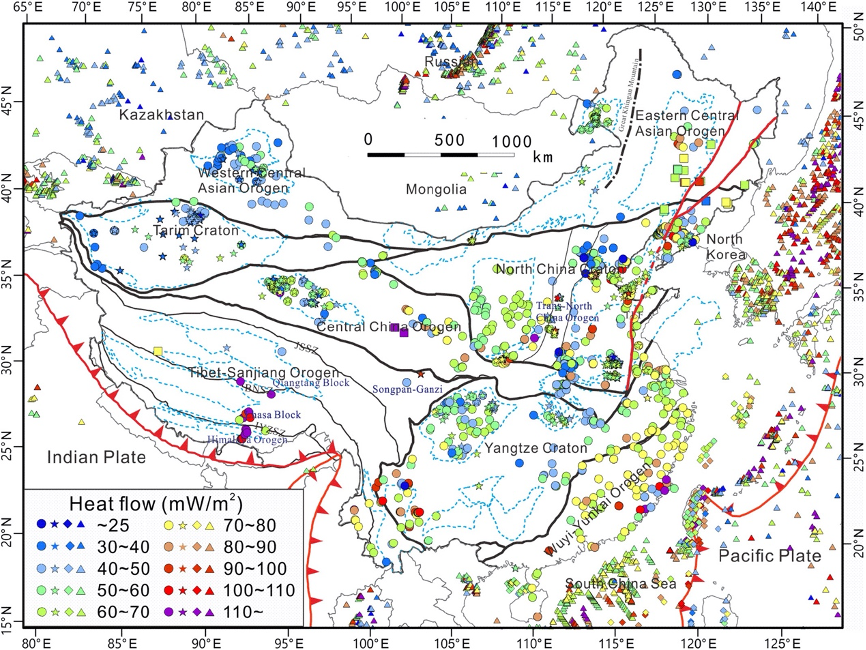
图 1 中国大地热流分布(Jiang et al. 2019)
热流值获取存在的问题
由于大地热流值并不能直接通过测量获得,而是通过地温梯度和地层热导率计算获得,因此地温梯度和地层热导率的精度就直接影响了大地热流值的准确性。因此在热流值的求取过程中,不可避免地出现以下的问题:
(1)由于地层热导率是通过岩芯测试获得的,所以其成本是非常高昂的,而且施工工艺复杂。需要通过取芯钻井或井壁取芯等手段获得地层样本,才能经实验室测试分析获得地层热导率。因此,岩芯分析的样本只能是离散的,不能反映整个井段的地层热导率信息。同时,取样后测试分析热导率,缺失了地层温度和压力的影响[12],无法反应地层真电阻率;
(2)主流测井装备并不将温度测量作为主要的技术指标,同时也缺乏对温度传感器的刻度标定,另外在测井过程中因为速度往往较快,故温度传感器并不能充分反映所在深度的真实温度。同时,由于常规测井仪中温度传感器分辨率不高,而且受到井的生产状态、流体类型、套管和水泥环等影响,井温测井也难以反映地层的真实温度。
鉴于此,可提出一种基于地层元素测井和高精度井温测井,并辅以校正算法,在没有岩芯或缺乏岩芯的情况下完成大地热流值的获得。
利用地层元素测井获取地层热导率
热导率是物体导热能力的刻度,是物质本身具有的特性。因此,通过分析地层各个组分的热导率,再用数学算法将其重构为地层的热导率便是可行的。对于地层来说,通过矿物恢复地层骨架热导率,再与地层流体的热导率结合,便可以获得地层的热导率。
岩石热导率与其矿物组分
地层中包含了各种矿物组分以及流体,地层流体及各种矿物组分的热导率是可以通过实验室获取的[13],地层热导率可以通过各组分的热导率合成而成[14]。可以通过分散模型计算,如:
\[\begin{matrix} \lambda_{B} = \lambda_{1}V_{1} \cdot \lambda_{2}V_{2} \cdot \cdots \cdot \lambda_{n}V_{n}\ \left( \text{\ 2\ } \right) \\ \end{matrix}\]式中:$\lambda_{B}$为岩石总体热导率,
$\lambda_{1}$,$\lambda_{2}$,……,$\lambda_{n}$分别为组成沉积岩各组分的热导率,
$V_{1}$,$V_{2}$,……,$V_{n}$为组成沉积岩个组分的体积百分比。
如果能通过井下测量获得各地层的矿物组成,就可以根据式2进行地层综合热导率的运算。地层元素测井为我们提供了通过测井方式获得地层矿物组成的手段。
地层元素测井
地层元素测井是一种地球化学测井,通过测量中子与地层物质的原子核发生作用放出的γ射线,得到元素含量进而确定矿物含量[15]。该测井方法由斯伦贝谢公司率先推出相关仪器,目前我公司也已经研发出了基于同位素中子源和可控源的地层元素测井仪器[16,17]。这种仪器能同时测量记录非弹性散射与俘获时产生的瞬发γ射线,利用剥谱分析直接得到地层元素 H、Cl 、Si 、Ca 、Fe 、S、Ti、Gd、Mg、B 和 C等,通过氧化物闭合模型和综合处理解释可定量得到地层的矿物含量,进而对储层的敏感性矿物进行识别。
地层中的每种矿物均有极其固定的化学元素成份,包括石英、方解石、白云石等,岩石则由不同的矿物所组成。通过地层元素测井可以反演获得矿物组成及其含量。地层元素测井矿物分析结果与取芯分析之间的误差小于15%[18]。
地层热导率的获得
在获得地层矿物组成之后,通过查询各矿物的热导率可以利用式2,合成地层热导率。需要注意的是热导率是受到温度和压力影响的[11,13],因此将岩石及水在常温下的热导率回归为特定温度压力(地层环境)下的热导率是能否精确获得地层热导率的关键。
首先考虑温度对热导率的影响,可以通过计算,将20℃下的热导率回归到特定温度下的热导率[19],算法如:
\[\begin{matrix} \lambda_{M,T} = \frac{293\lambda_{M,20}}{273 + T}\ \left( \text{\ 3\ } \right) \\ \end{matrix}\]式中:$\lambda_{M,T}$(W/m·K)为岩石在$T$(℃)时的固体骨架热导率,
$\lambda_{M,20}$为20℃时岩石骨架的热导率。
地层热导率在受到温度影响的同时也受到压力的影响,通常岩石的原始结构越疏松其热导率随压力递增的效应越显著[11]。其原因是压力使岩石趋于致密,减少声子发散源,使晶格振动过程中能量转移的效能提高,同时岩石在受压过程中,其颗粒的排列趋于紧密,孔隙缩小,部分裂隙趋于封闭,岩石的相结构逐渐趋于单一,增强了固体传热的效果,也是地层热导率增加的原因。为了考虑压力对热导率的影响,可以在公式2计算复合热导率之前,先求出每一种矿物组分在承压下的热导率,也可以在完成$\lambda_{M,T}$岩石骨架热导率计算后,根据岩性考虑压力带来的热导率的影响。可以通过实验,获得各类岩石的压力与热导率的关系,进行校正并获得承压条件下的地层骨架热导率$\lambda_{M,T}^{‘}$。图2为钙质粉砂岩和变质凝灰岩的压力—热导率关系图。
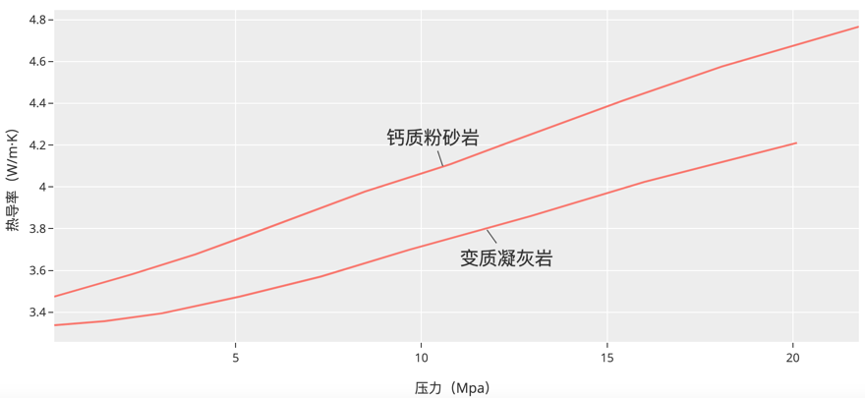
图 2 压力对热导率的影响(赵永信等,1995)
水的热导率也随温度变化,其变化规律如下式4和5:
\[\begin{matrix} \lambda_{W,T} = 0.56 + 0.0037T^{0.827}\ldots\ldots(0 \leq T \leq 63)\ \left. (\ \text{4}\ \right.) \\ \end{matrix}\] \[\begin{matrix} \lambda_{W,T} = 0.481 + 0.942lnT\ldots\ldots(T > 63)\ \left. (\ \text{5}\ \right.) \\ \end{matrix}\]式中:$\lambda_{W,T}$为$T$(℃)温度下水的热导率。
进一步可以通过地层骨架以及流体流体二者的热导率的叠加可以获得地层的热导率:
\[\begin{matrix} \lambda = \lambda_{M,T}^{'}(1 - \Phi)\lambda_{W,T}\Phi\ \left. (\ \text{6}\ \right.) \\ \end{matrix}\]式中:$\Phi$为地层孔隙度。
综上,通过地层元素测井方法,测量获取了地层矿物组分之后,可以通过相关算和对温度、压力的校正,得到地层热导率。
利用高精度温度测井获取地层温度
地温梯度的获得目前主要依赖于温度测井,但由于井温测井会涉及到温度曲线为非稳态等问题,因此井筒温度不能不能完全代表地层温度[20]。如何得到地层的真实温度,就成了获取地温梯度的主要问题。要解决这个问题可以从两个方面入手:一方面应在闭井后静置较长的时间使井筒温度接近地层温度,并使用高精度温度测井方法获得井温曲线;另一方面,可以通过校正的方式,推算地层温度。
高精度井温测井装备
在地下资源勘探开发过程中,地球物理测井技术可对开发地层进行地层物理参数的采集,这些参数包括地层岩石导电性质、岩石弹性、岩石原子物理性质等,以便进行后续的资源的开发方案的确立。地层的热力学性质也在测井采集的范围之内[21]。故目前测井设备一般均会测量井温参数,但由于测井仪器(主要指常规石油测井装备)的温度传感器并不进行刻度,而仅仅是进行对地层信息进行定性采集和分析,故传统的测井装备中温度曲线不宜直接用来表征地层温度。
现有的地温测井仪器多利用仪器内置的感温探头对温度进行采集,所采集的温度为梯度井温。这种温度采集方式存在两个显著缺陷:一、温度探头位于仪器外壳内部,对温度的感应存在一定滞后;二、梯度井温体现的是温度随井深变化,在局部地层温度异常时,其探测精度还有限。为了提高井温测量的精度,应该设计一种更精确的高精度井温探测仪。
可以设计一种高精度井温探测仪,解决目前高精度井温测量的问题[22]。高精度井温探测仪,在仪器的外壳上设置了4个温度探测器,每一个温度探测器由硬质高效导热合金和高灵敏度温度传感器组成。4个温度探测器通过不同的信号处理组合可以测量一个梯度井温和3个微差井温。为了提高测量的精确性,仪器配备偏心弹簧,可以保证仪器的测温探测器一侧贴靠井壁。另外,分布式光纤测温系统亦可在用来进行全井段温度采集[23–25]。使用分布式光纤测温系统,可以避免传统的生产测井井下测量仪器的电子线路工作在高温、高压的恶劣环境下仪器极易出现故障的问题。相关技术内容这里不做赘述。
地层温度的计算
不管通过任何一种测井方式获得的温度均为井内温度,其与地层温度仍存在差异。不论是钻孔完井后的测井,还是生产井测井,钻孔周边地层受到泥浆或井内生产流体的影响,温度场会产生变化,这种变化可以通过传热学研究进行校正。
事实上从20世纪50年代以来,就有诸多对多孔介质热传导的研究,尤其是针对油气生产井和回灌井的热传导研究[26,27]。其中Ramey的研究最为经典[28],后人也在其方法基础上做了很多发展,并形成了更加适用于井眼热传导研究的方法[29–32]。井眼及其周边温度场分布的性质可以如图 3所示,整个系统由井筒区、热表皮区(含套管、环空、水泥环等)及地层三部分组成。
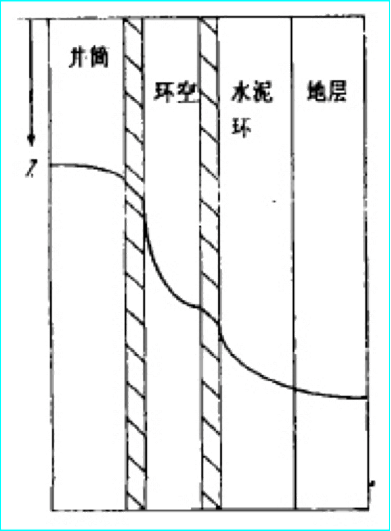
图 3 井孔和地层温度分布曲线(卢德唐等,2002)
根据Ramey方法,可以将系统的径向传热看成两个部分,分别是井内流体到水泥环外缘的一维稳定传热和水泥环外缘到地层之间的一维不稳定传热,进一步可以根据热传导理论得到井筒热损失的计算模型。实际的计算中,要考虑诸多假设,比如井内流体的相态以及温度响应的稳态等等,还需要根据实际情况做诸多调整。
总结
通过地层元素测井和高精度温度测井获得地层热导率的方法,可以不通过采样分析就能相对简单的获得地层的热导率,能够极大地丰富大地热流数据,为地热能勘查开发、地球动力学等研究提供基础数据。这种方式的主要优势有:
-
避免大量的取芯和实验室测试,就能获得较为准确的热导率数据;
-
可以获得连续的全井段的热导率数据,而岩芯分析仅能获得离散的数据;
-
利用油田大量的钻井资源,可以通过测井对地层热导率进行普查,从而获得更丰富的大地热流数据,直接指导油区的地热资源勘探与开发;
-
可以直接计算获得原地热导率(即所在地层温度下的热导率),实际上比试验测试获得的热导率更符合客观实际。
通过测井方法获取大地热流值的这个思路,不但可以解决我国目前大地热流值数据覆盖率地的问题,也可以利用油田现有的技术开拓出一种新的应用领域。这种方法可以推广到国土普查、地热资源开发、油气生成研究等诸多方面,将可成为对地下资源精细利用的有利武器。
参考文献
[1] Balling N. Heat flow and thermal structure of the lithosphere across the Baltic Shield and northern Tornquist Zone[J]. Tectonophysics, 1995, 244(1–3): 13–50.
[2] Furlong K P, Chapman D S. Heat Flow, Heat Generation, and the Thermal State of the Lithosphere[J]. Annual Review of Earth and Planetary Sciences, 2013, 41(1): 385–410.
[3] Smith C. Thermal hydrology and heat flow of Beowawe geothermal area, Nevada[J]. GEOPHYSICS, 1983, 48(5): 618–626.
[4] Davies J H, Davies D R. Earth’s surface heat flux[J]. Solid Earth, Copernicus GmbH, 2010, 1(1): 5–24.
[5] Davies J H. Global map of solid Earth surface heat flow[J]. Geochemistry, Geophysics, Geosystems, Wiley Online Library, 2013, 14(10): 4608–4622.
[6] 汪集旸, 黄少鹏. 中国大陆地区大地热流数据汇编[J]. 地质科学, 1988, 2: 196–204.
[7] 汪集旸, 黄少鹏. 中国大陆地区大地热流数据汇编(第二版)[J]. 地震地质, , 12(04): 351–363.
[8] 胡圣标, 何丽娟, 汪集旸. 中国大陆地区大地热流数据汇编 (第三版)[J]. 地球物理学报, 2001, 44(05): 611–626.
[9] 姜光政, 高堋, 饶松, 等. 中国大陆地区大地热流数据汇编 (第四版)[J]. 地球物理学报, 2016, 59(8): 2892–2910.
[10] Jiang G, Hu S, Shi Y, 等. Terrestrial heat flow of continental China: Updated dataset and tectonic implications[J]. Tectonophysics, 2019, 753: 36–48.
[11] 赵永信, 杨淑贞, 张文仁, 等. 岩石热导率的温压实验及分析[J]. 地球物理学进展, 1995(01): 104–113.
[12] Abdulagatov I M, Emirov S N, Abdulagatova Z Z, 等. Effect of pressure and temperature on the thermal conductivity of rocks[J]. Journal of Chemical & Engineering Data, ACS Publications, 2006, 51(1): 22–33.
[13] 苗社强, 李和平, 陈刚. 高温高压下矿物岩石热导率的实验研究进展[J]. 地球物理学进展, 2013, 28(05): 2453–2466.
[14] 王良书, 熊振, 郭随平, 等. 利用地球物理测井资料计算油气盆地中沉积岩原地热导率[J]. 石油地球物理勘探, 1999(05): 526-531+606.
[15] 郭宇, 杜洋. 地层元素测井技术的发展及其应用[J]. 西部探矿工程, 2017, 29(07): 78-81+88.
[16] 岳爱忠, 朱涵斌, 何绪新, 等. FEM地层元素测井仪[J]. 石油科技论坛, 2016, 35(S1): 20-24+238.
[17] 岳爱忠, 王树声, 何绪新, 等. FEM地层元素测井仪研制[J]. 测井技术, 2013, 37(04): 411–416.
[18] 袁祖贵, 成晓宁, 孙娟 AD 石油大学资源与信息学院 胜利石油管理局档案管理中心. 地层元素测井(ECS)——一种全面评价储层的测井新技术[J]. 原子能科学技术, 2004(S1): 208–213.
[19] Brigaud F, Chapman D S, Le Douaran S. Estimating thermal conductivity in sedimentary basins using lithologic data and geophysical well logs[J]. AAPG bulletin, GeoScienceWorld, 1990, 74(9): 1459–1477.
[20] 麦瑞天. 利用电测井温数据和计算法求取地层温度[J]. 石油钻采工艺, 1987(05): 37–44.
[21] Shakirov A, Chekhonin E, Popov Y, 等. Rock thermal properties from well-logging data accounting for thermal anisotropy[J]. Geothermics, Elsevier, 2021, 92: 102059.
[22] 沐杰, 王志刚, 谢迎春, 等. 一种高精度井温探测仪: 中国, CN209494559U[P]. 2019.
[23] 姜明顺, 隋青美, 林宗强. 分布式光纤测温系统在石油测井中的应用[J]. 光纤与电缆及其应用技术, 2007(02): 29–31.
[24] 刘媛, 雷涛, 张勇, 等. 油井分布式光纤测温及高温标定实验[J]. 山东科学, 山东省科学院, 2008(2008 年 06): 40–44.
[25] 朱鸿, 袁其祥. 分布式光纤测温技术在油田开发中的应用[J]. 胜利油田职工大学学报, 2009, 23(01): 42-43+72.
[26] Lesem L B, Greytok F, Marotta F, 等. A method of calculating the distribution of temperature in flowing gas wells[J]. Transactions of the AIME, Society of Petroleum Engineers, 1957, 210(01): 169–176.
[27] Moss J T, White P D. How to calculate temperature profiles in a water-injection well[J]. Oil and Gas J, 1959, 57(11): 174.
[28] Ramey Jr H J. Wellbore heat transmission[J]. Journal of petroleum Technology, Society of Petroleum Engineers, 1962, 14(04): 427–435.
[29] 卢德唐, 曾亿山, 郭永存 AD 中国科学技术大学力学系 中国科学技术大学力学系. 多层地层中的井筒及地层温度解析解[J]. 水动力学研究与进展(A辑), 2002(03): 382–390.
[30] Durrant A J, Thambynayagam R K M. Wellbore heat transmission and pressure drop for steam/water injection and geothermal production: a simple solution technique[J]. SPE Reservoir Engineering, Society of Petroleum Engineers, 1986, 1(02): 148–162.
[31] Hagoort J. Ramey’s wellbore heat transmission revisited[J]. SPE journal, Society of Petroleum Engineers, 2004, 9(04): 465–474.
[32] Kolo I, Sousa R, Zhang T. Heat Transmission in a Geothermal Wellbore: Modelling and Application[A]. Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia[C]. 2014.